| printed representation | box and pointer diagram |
|---|---|
| (a b (c d) ()) | 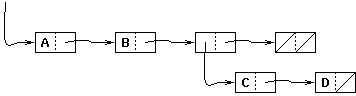
|
| (a b (c) ((d) e f) g) | 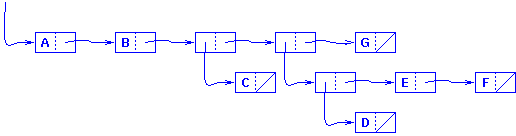
|
| ((a b) c d (e (f g))) | 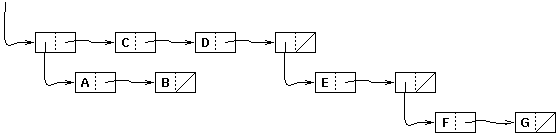
|
| Evaluate the Following (2 points each) | |
|---|---|
| expression | value |
| (cons '(a b c) '(d e f)) | ((a b c) d e f) |
| (list '(a b c) '(d e f)) | ((a b c) (d e f)) |
| (caddr '(a b (c d) e f)) | (c d) |
| (map even? '(1 2 3 4)) | (#f #t #f #t) |
(let ((a 1))
(let ((a 2)
(b (+ a 2)))
(list 'a a 'b b)))
| (a 2 b 3) |
(define (a-to-1 wd) (if (equal? wd 'a) 1 0)) (define (neato fn lst) (cond ((null? lst) 0) ((not (list? lst)) (fn lst)) (else (+ (neato fn (car lst)) (neato fn (cdr lst)))))) (define (foo expr) (neato a-to-1 expr)) |
-
What does (foo '(a b c (a d) a)) return? (5 points)
3 - In one short English sentence, what does foo do? (5 points)
Counts occurances of the symbol a within its argument.
- Define bar, which adds up all the numbers in an
s-expression, ignoring any non-numbers. Eg (bar '(a 1 2 (3
b))) gives 6. Use neato from above to make
your definition very simple. (5 points)
(define (bar s) (neato (lambda (x) (if (number? x) x 0)) s))
Examples:
((curry + 3) 1) ; 4 ((curry cons 'dog) '(cat rat)) ; (dog cat rat) (let ((f (curry assoc 'blood))) (f '((hair brown)(blood red)(tongue pink)))) ; (blood red)
(define (curry f x) (lambda (y) (f x y)))
Example:
(replace '(a b c (a d) a) 'a 'aye) ; (aye b c (aye d) aye)
The key here is that the base case is when E is not a pair, ie when it is a word or the empty list. You see this by thinking about very simple test cases, eg (replace 'x 'a 'aye).
(define (replace e a b)
(cond ((pair? e) (cons (replace (car e) a b)
(replace (car e) a b)))
((equal? e a) b)
(else e)))
Examples:
(reshape 'a '((((1))))) ; 1
(reshape '((((a)))) '1) ; ((((1))))
(reshape '(((a (b)))) '((1) 2)) ; (((1 (2))))
(reshape '(((a (b))) (c d))
'((1) (2 (((3))) 4))) ; (((1 (2))) (3 4))
The first thought is to do a simple recursion, but then you notice that the car of the first arg might have more words in it than the car of the second argument.
There are three main solution strategies. The first uses coroutines, implemented by continuations represented by passing around lambda's. This is elegant, but quite advanced.
A second strategy is to first build a table that describes the mapping from words in the first argument to words in the second argument, and then carry the mapping around while recursing through the first argument.
(define (flatten x)
(cond ((null? x) '())
((pair? x) (append (flatten (car x))
(flatten (cdr x))))
(else (list x))))
(define (reshape a b)
(substitute a
(map list (flatten a) (flatten b))))
(define (substitute a alist)
(let ((x (assoc a alist)))
(cond (x (cadr x))
((pair? a) (cons (substitute (car a) alist)
(substitute (cdr a) alist)))
(else a))))
This has a serious problem: what if the same word occurs twice in the
first argument? A case like this
(reshape '(a a) '((1 (2)))) ; (1 2)won't work, it will return (1 1) instead. Oops.
One way to solve this problem is to tag each of the words in the first argument with a unique identifier, both when flattening it and in place. Here we use as a tag the binary number whose digits describe the sequence of car's and cdr's required to get to the word, with car being a 0 and cdr being a 1, and with a leading 1 to eliminate ambiguity between eg 010 and 0010. This leads to the modified code
(define (reshape a b) (substitute (tag-words a 1) (map list (flatten-and-tag a 1) (flatten b)))) (define (tag-words a k) (cond ((null? a) a) ((pair? a) (cons (tag-words (car a) (* k 2)) (tag-words (cdr a) (+ (* k 2) 1)))) (else (list k a)))) (define (flatten-and-tag a k) (cond ((null? a) '()) ((pair? a) (append (flatten-and-tag (car a) (* k 2)) (flatten-and-tag (cdr a) (+ (* k 2) 1)))) (else (list (list k a)))))This is a little bit odd, as we're taking care to preserve the original words in the first argument as we tag them, but we don't actually care what the words within the first argument are! Instead of tagging them, we could just replace them with unique words and then build the alist as before. This simplifies the code:
(define (reshape a b)
(let ((unique-a (replace-words a 1)))
(substitute unique-a
(map list
(flatten unique-a)
(flatten b)))))
(define (replace-words a k)
(cond ((null? a) a)
((pair? a) (cons (replace-words (car a) (* k 2))
(replace-words (cdr a) (+ (* k 2) 1))))
(else k)))
Yet another strategy is to flattten out the second arg and then parcel out its elements as needed while recursing through the first argument. Then there is a problem: how to take the right number of elements off of the list before sending it down to the cdr case? This can be solved in two ways: one way is to compute how many are needed by the car case and strip them off of the list being passed to the cdr case:
(define (reshape a b) (reshape-aux a (flatten b))) (define (reshape-aux a lis) (cond ((null? a) '()) ((pair? a) (cons (reshape-aux (car a) lis) (reshape-aux (cdr a) (nth-cdr (count-words (car a)) lis)))) (else (car lis)))) ;;; This could equally well be defined as (count (flatten a)) (define (count-words a) (cond ((null? a) 0) ((pair? a) (+ (count-words (car a)) (count-words (cdr a)))) (else 1))) (define (nth-cdr n lis) (if (= n 0) lis (nth-cdr (- n 1) (cdr lis))))Unfortunately that is sometimes rather inefficient, since it counts the words in sublists over and over and over. The complexity comes out to O(n2), where n is the size of the first arg.
Instead we can actually pull elements off as they're needed. The insight is that the function that does the substitution knows how many elements it needed, so it should return not only the structure with the new words substituted in, but also a list of the remaining words to be substituted in.
(define (reshape a b)
(car (reshape-aux a (flatten b))))
;;; This returns a list of two elements:
;;; 1 - the structure A with elements from LIS substituted in
;;; 2 - LIS with the used elements popped off
(define (reshape-aux a lis)
(cond ((null? a) (list a lis))
((pair? a) (let ((x (reshape-aux (car a) lis)))
(let ((y (reshape-aux (cdr a) (cadr x))))
(list (cons (car x) (car y))
(cadr y)))))
(else (list (car lis)
(cdr lis)))))
Efficient, short, and sweet!