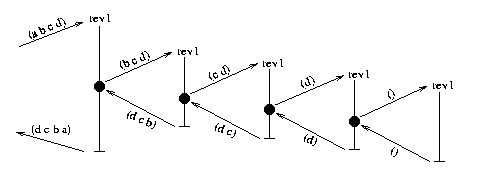
and when executing the rightmost invocation of rev1, the computer must store the entire chain of arrows leading to the left.
For example, the call to bar within this definition of foo is tail-recursive:
(define (foo x y)
(if (equal? x y)
(bar (car x) 'y 0)
'something))
When a procedure is defined recursively, and all its calls to itself are tail-recursive calls, then that procedure is itself called tail-recursive.
So the following function is not tail-recursive:
(define (rev1 lis)
(if (null? lis)
lis
(append (rev1 (cdr lis))
(list (car lis)))))
while the auxiliary function used here is tail-recursive:
(define (rev2 lis)
(rev2-aux '() lis))
(define (rev2-aux end-of-result to-be-reversed)
(if (null? to-be-reversed)
end-of-result
(rev2-aux (cons (car to-be-reversed)
end-of-result)
(cdr to-be-reversed))))
(To be technical, in the tail-recursive case the compiler would deallocate the current stack frame which holds the variable bindings of the current function invocation before the branch, while in the non-tail-recursive case these binding cannot be discarded, as they will be used again after the function being called returns.)
All Scheme implementations are required to perform the above optimization. (Some C compilers will do this too, while others, in particular gcc 2.7 and below, do so only when a procedure makes a tail-recursive call to itself.)
When we draw the call graph for the above code, as in the notes on helper functions, we can think of the arrows pointing back, which indicate where the result of a function will be returned to, to skip past tail-recursive invocations.
So for rev1 the call graph looks like this

and when executing the rightmost invocation of rev1, the
computer must store the entire chain of arrows leading to the left.
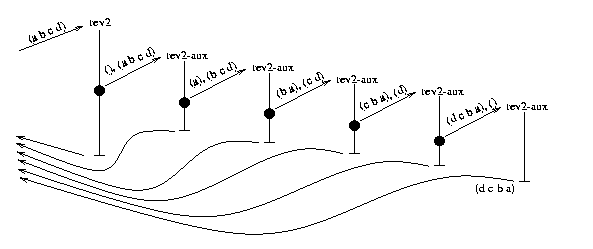
On the other hand, for rev2 and its helper function
rev2-aux, the call graph has return arrows that skip over
tail-recursive calls, so the computer ends up storing only one return
arrow rather than an entire chain of them.
Here is some spaghetti code:
L1:
(foo)
(bar)
(if (gronk) (goto L3) (goto L4))
L2:
(baz)
(rubber)
(tire)
(if (grink) (goto L1) (goto L2))
L3:
(dog)
(cat)
(if (rat) (goto L2) (goto L4))
L4:
(bat)
(if (hat) (goto L4) (goto L3))
We can translate this mechanically into goto-less code with
tail-recursive procedure calls:
(define (L1) (foo) (bar) (if (gronk) (L3) (L4))) (define (L2) (baz) (rubber) (tire) (if (grink) (L1) (L2))) (define (L3) (dog) (cat) (if (rat) (L2) (L4))) (define (L4) (bat) (if (hat) (L4) (L3)))
Fibb:
(set! i 1)
(set! f_im1 1)
(set! f_i 1)
L2:
(if (= i n)
(return f_i)
(let ((new (+ f_i f_im1)))
(set! f_im1 f_i)
(set! f_i new)
(set! i (+ i 1))
(goto L2)))
We can translate this into Scheme, with goto replaced by
tail-recursive procedure calls, return replaced by Scheme's implicit
returns, and the assignments replaced by binding.
(define (fibb n)
(fibb-L2 n 1 1 1))
(define (fibb-L2 n i f_im1 f_i)
(if (= i n)
f_i
(let ((new (+ f_i f_im1)))
(fibb-L2 n
(+ i 1)
f_i
new))))
Similarly, if we want to add up the first n squares,
S(n)=12+22+32+42+...+n2,
we can note that S(n)=S(n-1)+n2, and use this
insight to make a recursive definition
(define (S n)
(if (= n 0)
0
(+ (S (- n 1)) (* n n))))
but this non-tail-recursive function would require a great deal of
intermediate storage to calculate (S 40000000). Instead we
can use a tail-recursive definition, by using a helper function
Saux which is defined by
Saux(n,a)=a+12+22+32+42+...+n2,
and note the two properties S(n)=Saux(n,0) and
Saux(n,a)=Saux(n-1,a+n2), which allows us to make
a tail-recursive definition
(define (S n) (Saux n 0))
(define (Saux n a)
(if (= n 0)
a
(Saux (- n 1) (+ a (* n n)))))
Which is tail-recursive and therefore does not consume inordinate
storage when called with a large argument.