Problem Set Eight, CS 257

Due at 11:59pm on Thursday Apr 22, 1999

[Software] quality has much in common with sex. Everybody is for it. (Under certain conditions, of course.) Everyone feels they understand it. (Even though they wouldn't want to explain it.) Everyone thinks execution is only a matter of following natural inclinations. (After all, we do get along somehow.) And, of course, most people feel that problems in these areas are caused by other people. (If only they would take the time to do things right.)

Philip Crosby

This is more of a programming project than just a problem set.

Goal

write a simple Scheme Graphing Calculator.

Interface

The interface is quite Scheme-y, you do not need any flashing input thing. Users just type expressions to Scheme, but you have defined some nice functions that they can use.

First, they need a ``little language'' in which to write their mathematical expressions to be plotted. This language is minimal:

a (real) number is an expression in the language
the symbol x is an expression in the language
(boperator expression expression) is an expression in the language, where boperator is either * or +
(uoperator expression) is an expression in the language, where uoperator is either sin, cos, or exp.

Note that in this little language the arithmetic operators always take exactly two arguments, and there is no subtraction. So to subtract the cosine of x from e to the x cubed you would use (+ (exp (* (* x x) x)) (* -1 (cos x))). The trigonometric functions take their arguments in radians, for ease of implementation and ease of calculating derivatives. Also note that the only ``variable'' is x; we will not need any more. (The simplicity of this little language makes your job easier.)

Here are the functions you need to write:

Define ceval which, given an expression in the little languag above and a value for x, returns the appropriate numeric result. Eg (ceval '(* x (+ x 1)) 2) yields 6. Note: do not call the system eval in your code.
Define cdiff which takes an express in the little language above and returns its symbolic derivative with respect to x, in the little language above. (For extra credit, make sure the expression returned is simplified, without sacrificing correctness of course.)
Define graph which takes an expression in the little language above, along with an x minimum and maximum, a y minimum and maximum, and a number of points to evaluate n. It returns a graphic object which is a plot of the given expression over the given range, with the y axis covering the given range. The expression passed should be evaluated at the given number of points, evenly spaced along the x axis in the range given, and the while thing should be surrounded by a nice box. (For extra credit, allow the user to pass #t for either of the y axis bounds, and in that case you should automatically calculate that part of the y bound to fit the data.)
You don't need to label the axes or put in tic marks or such.
Example: (graph '(* (sin x) (* x x)) -20 20 -300 300 200) would plot x²sin x from x=-20 to 20, with the y axis running from -300 to 300, and would evaluate the expression at 200 x points. It would produce a graphic object that looks about like this:
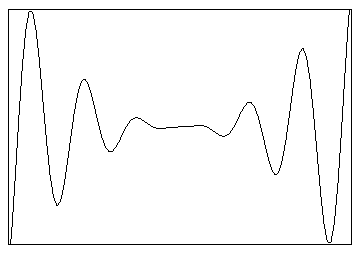
Define dgraph which is just like graph except that it takes an additional argument right after the expression, which is how many derivatives of the function to plot. So for instance (dgraph '(* (sin x) (* x x)) 0 -20 20 -300 300 200) does exactly the same as the previous example, while (dgraph '(* (sin x) (* x x)) 2 -20 20 -300 300 200) would, in addition to the information on the graph described above, would also put onto the plot a curve for the first derivative of x² sin x, namely x² cos x + 2 x sin x, as well as the second derivative, - x² sin x + 4 x cos x + 2 sin x.

Barak Pearlmutter <bap@cs.unm.edu>